what phase of the moon must it be to have a solar eclipse?

Calculation and prediction of eclipses

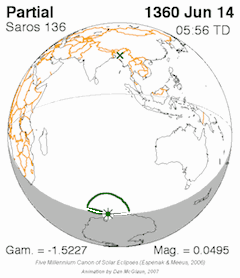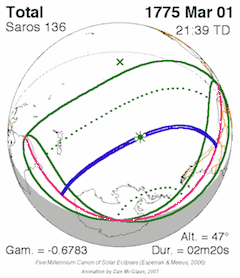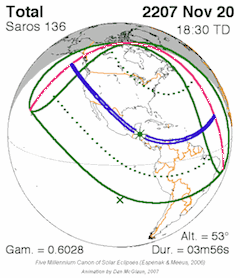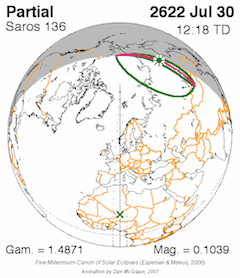
Paths of partially, annularity, hybridity, totality and partially for Solar Saros Series 136. The interval betwixt successive eclipses in the series is i saros, approximately eighteen years.

Eclipses may occur repeatedly, separated past certain intervals of fourth dimension: these intervals are called eclipse cycles.^[i] The series of eclipses separated past a repeat of one of these intervals is called an eclipse serial.

Eclipse weather [edit]

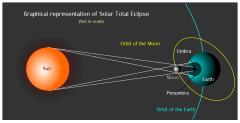
Eclipses may occur when Earth and the Moon are aligned with the Sun, and the shadow of 1 body projected by the Dominicus falls on the other. And so at new moon, when the Moon is in conjunction with the Sun, the Moon may pass in front of the Sunday every bit viewed from a narrow region on the surface of World and cause a solar eclipse. At full moon, when the Moon is in opposition to the Sunday, the Moon may pass through the shadow of Globe, and a lunar eclipse is visible from the night half of Earth. The conjunction and opposition of the Moon together have a special name: syzygy (Greek for "junction"), because of the importance of these lunar phases.

An eclipse does not occur at every new or full moon, considering the airplane of the Moon's orbit around World is tilted with respect to the plane of Earth's orbit around the Sun (the ecliptic): so as viewed from Globe, when the Moon appears nearest the Sun (at new moon) or furthest from it (at total moon), the three bodies are usually not exactly on the same line.

This inclination is on boilerplate about five° 9′, much larger than the apparent mean diameter of the Sun (32′ 2″), the Moon as viewed from Earth's surface directly below the Moon (31′ 37″), and Earth's shadow at the mean lunar distance (1° 23′).

Therefore, at most new moons, Earth passes too far north or south of the lunar shadow, and at most full moons, the Moon misses Earth's shadow. Besides, at near solar eclipses, the apparent angular bore of the Moon is insufficient to fully occlude the solar disc, unless the Moon is effectually its perigee, i.east. nearer Earth and apparently larger than boilerplate. In any case, the alignment must exist almost perfect to cause an eclipse.

An eclipse can occur merely when the Moon is on or near the aeroplane of Earth's orbit, i.due east. when its ecliptic latitude is depression. This happens when the Moon is around either of the two orbital nodes on the ecliptic at the time of the syzygy. Of class, to produce an eclipse, the Dominicus must likewise be around a node at that time – the same node for a solar eclipse or the reverse node for a lunar eclipse.

Recurrence [edit]

A symbolic orbital diagram from the view of the Globe at the centre, showing the Moon's 2 nodes where eclipses can occur.

Upwards to iii eclipses may occur during an eclipse season, a one- or two-month period that happens twice a yr, around the time when the Sun is near the nodes of the Moon'due south orbit.

An eclipse does not occur every month, because i month later an eclipse the relative geometry of the Sun, Moon, and Earth has inverse.

As seen from the Earth, the time it takes for the Moon to return to a node, the draconic month, is less than the time information technology takes for the Moon to return to the same ecliptic longitude as the Sun: the synodic month. The primary reason is that during the time that the Moon has completed an orbit around the Globe, the Earth (and Moon) have completed nigh i⁄13 of their orbit effectually the Sun: the Moon has to make up for this in order to come over again into conjunction or opposition with the Sunday. Secondly, the orbital nodes of the Moon precess westward in ecliptic longitude, completing a full circle in about xviii.threescore years, so a draconic month is shorter than a sidereal month. In all, the difference in menstruum betwixt synodic and draconic month is well-nigh two+ 1⁄three days. Likewise, equally seen from the Earth, the Sun passes both nodes as it moves along its ecliptic path. The period for the Sun to return to a node is called the eclipse or draconic year: about 346.6201 days, which is nigh 1⁄20 year shorter than a sidereal year because of the precession of the nodes.

If a solar eclipse occurs at ane new moon, which must be close to a node, then at the side by side total moon the Moon is already more than a day by its opposite node, and may or may not miss the Earth's shadow. By the side by side new moon it is even farther ahead of the node, and then information technology is less likely that there will be a solar eclipse somewhere on Globe. By the next month, in that location will certainly be no upshot.

Notwithstanding, near v or 6 lunations afterward the new moon volition fall close to the opposite node. In that time (one-half an eclipse twelvemonth) the Sun volition have moved to the reverse node also, then the circumstances will again be suitable for ane or more eclipses.

Periodicity [edit]

The periodicity of solar eclipses is the interval between any 2 solar eclipses in succession, which will be either 1, 5, or 6 synodic months.^[2] It is calculated that the earth will experience a total number of eleven,898 solar eclipses betwixt 2000 BCE and 3000 CE. A particular solar eclipse will be repeated approximately after every 18 years 11 days and 8 hours (6,585.32 days) of period, but not in the aforementioned geographical region.^[three] A particular geographical region will feel a particular solar eclipse in every 54 years 34 days menstruation.^[2] Total solar eclipses are rare events, although they occur somewhere on Earth every 18 months on boilerplate,^[iv]

Repetition of solar eclipses [edit]

For the repetition of a solar eclipse, the geometric alignment of the Earth, Moon and Sunday, as well equally some parameters of the lunar orbit should be repeated. The following parameters and criteria must be repeated for the repetition of a solar eclipse:

1. The Moon must be in new phase.
2. The longitude of perigee or apogee of the Moon must exist the same.
3. The longitude of the ascending node or descending node must be the aforementioned.
4. The Earth will be nearly the same altitude from the Sunday, and tilted to it in nearly the same orientation.

These weather condition are related with the three periods of the Moon'due south orbital motion, viz. the synodic month, anomalistic month and draconic month. In other words, a item eclipse will be repeated only if the Moon volition complete roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Globe-Sun-Moon geometry volition be nearly identical to that eclipse. The Moon will exist at the same node and the same distance from the Earth. Gamma changes monotonically throughout any single Saros serial. The alter in gamma is larger when Earth is near its aphelion (June to July) than when it is almost perihelion (December to January). When the Globe is nearly its average distance (March to April or September to Oct), the change in gamma is average.

Repetition of lunar eclipses [edit]

For the repetition of a lunar eclipse, the geometric alignment of the Moon, World and Sun, as well equally some parameters of the lunar orbit should be repeated. The post-obit parameters and criteria must exist repeated for the repetition of a lunar eclipse:

1. The Moon must be in full phase.
2. The longitude of perigee or apogee of the Moon must be the same.
3. The longitude of the ascending node or descending node must exist the same.
4. The Earth will be almost the same distance from the Lord's day, and tilted to it in nearly the same orientation.

These conditions are related with the three periods of the Moon'southward orbital movement, viz. the synodic month, anomalistic month and draconic month. In other words, a particular eclipse volition exist repeated merely if the Moon will complete roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will exist almost identical to that eclipse. The Moon will be at the same node and the same altitude from the Earth. Gamma changes monotonically throughout whatever single Saros serial. The change in gamma is larger when Earth is near its aphelion (June to July) than when information technology is near perihelion (Dec to Jan). When the Globe is virtually its average distance (March to April or September to Oct), the change in gamma is average.

Eclipses would non occur in every month [edit]

Another matter to consider is that the motion of the Moon is non a perfect circle. Its orbit is distinctly elliptic, and then the lunar distance from Earth varies throughout the lunar cycle. This varying distance changes the apparent diameter of the Moon, and therefore influences the chances, elapsing, and type (partial, annular, total, mixed) of an eclipse. This orbital period is called the anomalistic calendar month, and together with the synodic month causes the so-called "full moon cycle" of almost 14 lunations in the timings and appearances of full (and new) Moons. The Moon moves faster when it is closer to the Earth (well-nigh perigee) and slower when it is near apogee (furthest distance), thus periodically irresolute the timing of syzygies past up to fourteen hours either side (relative to their mean timing), and causing the apparent lunar angular bore to increase or subtract by most 6%. An eclipse cycle must comprise shut to an integer number of anomalistic months in order to perform well in predicting eclipses.

If the Earth had a perfectly circular orbit centered around the Sun, and the Moon's orbit was also perfectly circular and centered around the Earth, and both orbits were coplanar (on the same plane) with each other, and then two eclipses would happen every lunar month (29.53 days). A lunar eclipse would occur at every full moon, a solar eclipse every new moon, and all solar eclipses would be the same blazon. In fact the distances between the World and Moon and that of the Earth and the Lord's day vary because both the Earth and the Moon have elliptic orbits. Also, both the orbits are non on the aforementioned airplane. The Moon's orbit is inclined nearly 5.14° to Earth'due south orbit around the Sun. So the Moon's orbit crosses the ecliptic at two points or nodes. If a New Moon takes place within about 17° of a node, then a solar eclipse will be visible from some location on Earth.^{[v] [6] [7]}

At an boilerplate angular velocity of 0.99° per day, the Sun takes 34.5 days to cross the 34° wide eclipse zone centered on each node. Because the Moon's orbit with respect to the Sun has a mean duration of 29.53 days, there will always be one and perhaps two solar eclipses during each 34.5-day interval when the Sun passes through the nodal eclipse zones. These fourth dimension periods are chosen eclipse seasons.^[2] Either two or 3 eclipses happen each eclipse season. During the eclipse season, the inclination of the Moon'southward orbit is low, hence the Sunday, Moon, and Earth become aligned straight plenty (in syzygy) for an eclipse to occur.

Numerical values [edit]

These are the lengths of the various types of months as discussed above (according to the lunar ephemeris ELP2000-85, valid for the epoch J2000.0; taken from (e.g.) Meeus (1991) ):

SM = 29.530588853 days (Synodic calendar month)^[8]

DM = 27.212220817 days (Draconic month)^[ix]

AM = 27.55454988 days (Anomalistic month)^[x]

EY = 346.620076 days (Eclipse year)

Note that in that location are three chief moving points: the Sun, the Moon, and the (ascending) node; and that there are iii master periods, when each of the three possible pairs of moving points meet one another: the synodic month when the Moon returns to the Sun, the draconic calendar month when the Moon returns to the node, and the eclipse year when the Lord's day returns to the node. These iii two-way relations are not independent (i.e. both the synodic calendar month and eclipse year are dependent on the apparent motion of the Lord's day, both the draconic month and eclipse year are dependent on the motion of the nodes), and indeed the eclipse year can be described every bit the shell period of the synodic and draconic months (i.east. the period of the difference between the synodic and draconic months); in formula:

${\displaystyle {\mbox{EY}}={\frac {{\mbox{SM}}\times {\mbox{DM}}}{{\mbox{SM}}-{\mbox{DM}}}}}$

as tin be checked by filling in the numerical values listed in a higher place.

Eclipse cycles have a period in which a sure number of synodic months closely equals an integer or half-integer number of draconic months: i such menstruation after an eclipse, a syzygy (new moon or full moon) takes place over again near a node of the Moon's orbit on the ecliptic, and an eclipse can occur again. However, the synodic and draconic months are incommensurate: their ratio is not an integer number. We demand to estimate this ratio by mutual fractions: the numerators and denominators so requite the multiples of the ii periods – draconic and synodic months – that (approximately) span the same corporeality of time, representing an eclipse cycle.

These fractions can be found by the method of continued fractions: this arithmetical technique provides a series of progressively better approximations of whatsoever real numeric value by proper fractions.

Since there may exist an eclipse every half draconic month, nosotros need to detect approximations for the number of half draconic months per synodic month: so the target ratio to guess is: SM / (DM/ii) = 29.530588853 / (27.212220817/ii) = 2.170391682

The continued fractions expansion for this ratio is:

ii.170391682 = [two;5,1,6,1,1,1,1,1,11,1,...]:[eleven]          Quotients  Convergents            one-half DM/SM     decimal      named bike (if whatever)     2;           2/1    = two     5           11/5    = 2.ii     1           xiii/6    = two.166666667  semester     half dozen           89/41   = 2.170731707  hepton     ane          102/47   = 2.170212766  octon     i          191/88   = ii.170454545  tzolkinex     1          293/135  = 2.170370370  tritos     1          484/223  = 2.170403587  saros     one          777/358  = 2.170391061  inex    11         90314161 = 2.170391732     1         9808/4519 = ii.170391679   ...        

The ratio of synodic months per half eclipse twelvemonth yields the aforementioned serial:

v.868831091 = [5;1,6,1,1,1,i,1,11,1,...] Quotients  Convergents            SM/half EY  decimal        SM/total EY  named cycle     5;      5/1      = 5     1       half-dozen/one      = half-dozen              12/one        semester     6      41/7      = 5.857142857                hepton     1      47/viii      = 5.875          47/4        octon     1      88/15     = 5.866666667                tzolkinex     i     135/23     = 5.869565217                tritos     i     223/38     = 5.868421053   223/19       saros     1     358/61     = five.868852459   716/61       inex    eleven    4161/709    = 5.868829337     1    4519/770    = v.868831169  4519/385   ...        

Each of these is an eclipse cycle. Less authentic cycles may be constructed past combinations of these.

Eclipse cycles [edit]

This table summarizes the characteristics of various eclipse cycles, and can be computed from the numerical results of the preceding paragraphs; cf. Meeus (1997) Ch.9. More details are given in the comments below, and several notable cycles accept their ain pages.

Any eclipse cycle, and indeed the interval between any 2 eclipses, can be expressed as a combination of saros (s) and inex (i) intervals. These are listed in the column "formula".

Cycle	Formula	Solar days	Synodic months	Draconic months	Anomalistic months	Eclipse years	Tropical years	Eclipse seasons	Node
fortnight	nineteeni − 30+ 1⁄2 s	xiv.77	0.5	0.543	0.536	0.043	0.040	0.086	alternate
synodic calendar month	38i − 61south	29.53	1	1.085	i.072	0.085	0.081	0.17	same
pentalunex	53s − 33i	147.65	5	five.426	5.359	0.426	0.404	0.852	alternating
semester	5i − 8s	177.18	six	6.511	6.430	0.511	0.485	ane	alternate
lunar year	10i − xvis	354.37	12	13.022	12.861	1.022	0.970	2	same
hepton	5s − 3i	1210.73	41	44.485	43.952	three.485	3.321	vii	alternate
octon	iii − 3s	1387.94	47	51.004	fifty.371	4.004	three.800	8	same
tzolkinex	2due south − i	2598.69	88	95.497	94.311	7.497	seven.115	fifteen	alternate
sar (half saros)	one⁄2 s	3292.66	111.5	120.999	119.496	9.499	9.015	nineteen	same
tritos	i − due south	3986.63	135	146.501	144.681	11.501	10.915	23	alternating
saros (southward)	s	6585.32	223	241.999	238.992	18.999	18.030	38	same
Metonic cycle	teni − 15s	6939.69	235	255.021	251.853	20.021	19.000	40	same
inex (i)	i	10,571.95	358	388.500	383.674	30.500	28.945	61	alternate
exeligmos	3s	19,755.96	669	725.996	716.976	56.996	54.090	114	same
Callippic cycle	xli − 60s	27,758.75	940	1020.084	1007.411	lxxx.084	76.001	160	same
triad	3i	31,715.85	1074	1165.500	1151.021	91.500	86.835	183	alternate
Hipparchic cycle	25i − 21due south	126,007.02	4267	4630.531	4573.002	363.531	344.996	727	alternate
Babylonian	fourteeni + 2s	161,177.95	5458	5922.999	5849.413	464.999	441.291	930	same
tetradia (Meeus Iii)	22i − 4s	206,241.63	6984	7579.008	7484.849	595.008	564.671	1190	same
tetradia (Meeus [I])	19i + iis	214,037.70	7248	7865.500	7767.781	617.500	586.016	1235	alternating

Notes [edit]

Fortnight

Half a synodic month (29.53 days). When at that place is an eclipse, in that location is a off-white take chances that at the next syzygy at that place will be some other eclipse: the Dominicus and Moon will have moved near xv° with respect to the nodes (the Moon being opposite to where it was the previous time), only the luminaries may still be within bounds to brand an eclipse. For example, partial solar eclipse of June 1, 2011 is followed by the total lunar eclipse of June 15, 2011 and fractional solar eclipse of July 1, 2011.

For more information see eclipse season.

Synodic month

Similarly, 2 events i synodic month apart accept the Sun and Moon at 2 positions on either side of the node, 29° apart: both may crusade a partial eclipse. For a lunar eclipse, information technology is a penumbral lunar eclipse.

Pentalunex

five synodic months. Successive solar or lunar eclipses may occur 1, v or 6 synodic months apart.^[12]

Semester

Half a lunar yr. Eclipses will repeat exactly ane semester apart at alternating nodes in a cycle that lasts for 8 eclipses. Because information technology is close to a half integer of anomalistic, draconic months, and tropical years, each solar eclipse will alternate betwixt hemispheres each semester, as well as alternate between total and annular. Hence there tin be a maximum of i total or annular eclipse each in a given twelvemonth. (For a lunar eclipse, eclipses will repeat exactly one semester apart at alternating nodes in a bike that lasts for viii eclipses. Considering information technology is close to a one-half integer of anomalistic, draconic months, and tropical years, each lunar eclipse volition alternate between edges of Earth'south shadow each semester, also as alternate betwixt Lunar Perigee and Lunar Apogee. Hence there can be a maximum of one Lunar Perigee or Lunar Apogee each in a given year.)

Lunar year

Twelve (synodic) months, a piddling longer than an eclipse year: the Dominicus has returned to the node, so eclipses may once again occur.

Octon

This is 1⁄5 of the Metonic wheel, and a adequately decent short eclipse cycle, merely poor in anomalistic returns. Each octon in a series is two saros apart, e'er occurring at the same node. For solar (or lunar) eclipses, information technology is equal to 47 synodic months (1388 solar days).

Tzolkinex

Includes a half draconic month, and so occurs at alternating nodes and alternates between hemispheres. Each consecutive eclipse is a member of preceding saros series from the one earlier. Equal to ten tzolk'ins. Every tertiary tzolkinex in a series is most an integer number of anomalistic months and and so volition have similar backdrop.

Sar (half saros)

Includes an odd number of fortnights (223). As a result, eclipses alternate between lunar and solar with each cycle, occurring at the aforementioned node and with like characteristics. A solar eclipse with small gamma will be followed by a very cardinal total lunar eclipse. A solar eclipse where the moon's penumbra just barely grazes the southern limb of world will exist followed half a saros later past a lunar eclipse where the moon just grazes the southern limb of the earth'southward penumbra.^[13]

Tritos

A mediocre cycle, relates to the saros like the inex. A triple tritos is close to an integer number of anomalistic months and so volition have similar backdrop.

Saros

The best known eclipse wheel, and one of the best for predicting eclipses, in which 223 synodic months equal 242 draconic months with an fault of merely 51 minutes. Information technology is likewise shut to 239 anomalistic months, which makes the circumstances between two eclipses one saros apart very similar.

Metonic cycle or enneadecaeteris

This is nearly equal to 19 tropical years, but is also five "octon" periods and close to 20 eclipse years: and so it yields a curt series of eclipses on the same calendar engagement. It consists of 110 hollow months and 125 full months, so nominally 6940 days, and equals 235 lunations (235 synodic months) with an error of just effectually 7.five hours.

Inex

Very convenient in the classification of eclipse cycles. Inex series, after a sputtering beginning, keep for many thousands of years giving eclipses every 29 years or and then. I inex after an eclipse, another eclipse takes place at almost the aforementioned longitude, but at the opposite latitude.

Exeligmos

A triple saros, with the advantage that information technology has almost an integer number of days, and then the next eclipse volition exist visible at locations near the eclipse that occurred one exeligmos earlier, in dissimilarity to the saros, in which the eclipse occurs about 8 hours later in the twenty-four hours or about 120° to the west of the eclipse that occurred one saros earlier.

Callippic bike

441 hollow months and 499 full months; thus iv Metonic cycles minus i day or precisely 76 years of 365+ one⁄four days. It equals 940 lunations with an error of merely 5.9 hours.

Triad

A triple inex, with the advantage that information technology has near an integer number of anomalistic months, which makes the circumstances between two eclipses i Triad apart very similar, but at the contrary latitude. Well-nigh exactly 87 agenda years minus 2 months. The triad means that every 3rd saros series will exist like (mostly total fundamental eclipses or annular central eclipses for instance). Saros 130, 133, 136, 139, 142 and 145, for example, all produce mainly total central eclipses.

Hipparchic bike

Non a noteworthy eclipse cycle, but Hipparchus constructed it to closely match an integer number of synodic and anomalistic months, years (345), and days. Past comparing his ain eclipse observations with Babylonian records from 345 years before, he could verify the accuracy of the various periods that the Chaldeans used.

Babylonian

The ratio 5923 returns to latitude in 5458 months was used by the Chaldeans in their astronomical computations.

Tetradia

Sometimes four total lunar eclipses occur in a row with intervals of half-dozen lunations (semester), and this is called a tetrad. Giovanni Schiaparelli noticed that at that place are eras when such tetrads occur comparatively ofttimes, interrupted by eras when they are rare. This variation takes about vi centuries. Antonie Pannekoek (1951) offered an caption for this miracle and found a period of 591 years. Van den Bergh (1954) from Theodor von Oppolzer's Canon der Finsternisse found a period of 586 years. This happens to be an eclipse cycle; run across Meeus [I] (1997). Recently Tudor Hughes explained the variation from secular changes in the eccentricity of the Earth'southward orbit: the flow for occurrence of tetrads is variable and currently is nigh 565 years; see Meeus III (2004) for a detailed discussion.

Saros serial and inex series [edit]

Any eclipse can be assigned to a given saros series and inex series. The year of a solar eclipse (in the Gregorian calendar) is and then given approximately by:^[fourteen]

yr = 28.945 × number of the saros series + eighteen.030 × number of the inex serial − 2882.55

When this is greater than 1, the integer part gives the yr Advertizement, just when it is negative the year BC is obtained past taking the integer part and calculation 2. For instance, the eclipse in saros serial 0 and inex series 0 was in the middle of 2884 BC.

See also [edit]

• Saros (astronomy)

References [edit]

1. ^ properly, these are periods, not cycles
2. ^ ^{a b c} NASA Periodicity of solar eclipses
3. ^ van Gent, Robert Harry (8 September 2003). "A Catalogue of Eclipse Cycles".
4. ^ Solar Eclipses: 2011–2020
5. ^ Littmann, Mark; Fred Espenak; Ken Willcox (2008). Totality: Eclipses of the Dominicus. Oxford Academy Press. ISBN978-0-nineteen-953209-4.
6. ^ Periodicity of Lunar and Solar Eclipses, Fred Espenak
7. ^ Five Millennium Catalog of Lunar and Solar Eclipses: -1999 to +3000, Fred Espenak and Jean Meeus
8. ^ Meeus (1991) form. 47.1
9. ^ Meeus (1991) ch. 49 p.334
10. ^ Meeus (1991) grade. 48.ane
11. ^ 2.170391682 = ii + 0.170391682 ; 1/0.170391682 = 5 + 0.868831085... ; 1/0.868831085... = 1 +5097171...6237575... ; etc. ; Evaluating this 4th continued fraction: one/half dozen + 1 = 7/6; 6/vii + 5 = 41/7 ; 7/41 + two = 89/41
12. ^ A Catalogue of Eclipse Cycles, Robert Harry van Gent
13. ^ A Catalogue of Eclipse Cycles, Robert Harry van Gent
14. ^ Based on Saros, Inex and Eclipse cycles.

• S. Newcomb (1882): On the recurrence of solar eclipses. Astron.Pap.Am.Eph. vol. I pt. I . Agency of Navigation, Navy Dept., Washington 1882
• J.N. Stockwell (1901): Eclips-cycles. Astron.J. 504 [vol.xx1(24)], fourteen-Aug-1901
• A.C.D. Crommelin (1901): The 29-year eclipse cycle. Observatory xxiv nr.310, 379, October-1901
• A. Pannekoek (1951): Periodicities in Lunar Eclipses. Proc. Kon. Ned. Acad. Wetensch. Ser.B vol.54 pp. xxx..41 (1951)
• G. van den Bergh (1954): Eclipses in the 2d millennium B.C. Tjeenk Willink & Zn NV, Haarlem 1954
• G. van den Bergh (1955): Periodicity and Variation of Solar (and Lunar) Eclipses, two vols. Tjeenk Willink & Zn NV, Haarlem 1955
• Jean Meeus (1991): Astronomical Algorithms (1st ed.). Willmann-Bong, Richmond VA 1991; ISBN 0-943396-35-two
• Jean Meeus (1997): Mathematical Astronomy Morsels [I], Ch.ix Solar Eclipses: Some Periodicities (pp. 49..55). Willmann-Bell, Richmond VA 1997; ISBN 0-943396-51-4
• Jean Meeus (2004): Mathematical Astronomy Morsels III, Ch.21 Lunar Tetrads (pp. 123..140). Willmann-Bong, Richmond VA 2004; ISBN 0-943396-81-6

External links [edit]

• A Catalogue of Eclipse Cycles (more comprehensive than the above)
• Search five,000 years worth of eclipses
• Eclipses, Cosmic Clockwork of the Ancients
• The Saros and the Inex

griffincarringe.blogspot.com

Source: https://en.wikipedia.org/wiki/Eclipse_cycle

Share this post